Understanding the Corresponding Sides Definition: A Guide for Math Learners
Corresponding sides are an essential concept in geometry that students must learn to master. These sides are the matching sides of two similar figures, and they play a crucial role in determining the similarity of geometric shapes. Understanding corresponding sides is necessary not only for solving mathematical problems but also for real-life applications such as architecture and engineering. In this article, we'll explore the definition of corresponding sides in detail and provide examples to help you grasp this concept better.
In geometry, corresponding sides refer to the matching sides of two similar figures. Similar figures are those that have the same shape but may have different sizes. For example, two rectangles with different lengths and widths can still be considered similar if their angles are congruent. Corresponding sides are always proportional to each other, meaning that they have the same ratio of length or width.
One way to identify corresponding sides is to match the vertices of the figures. Each vertex of one figure corresponds to a vertex in the other figure, and the sides that connect these vertices are the corresponding sides. For instance, if we have two triangles ABC and DEF, where angle A=angle D, angle B=angle E, and angle C=angle F, then side AB corresponds to side DE, side AC corresponds to side DF, and side BC corresponds to side EF.
Another way to identify corresponding sides is to use the notation method. This method involves labeling the sides of the two figures with the same letters, but with a prime symbol (') to indicate that they belong to a different figure. For example, if we have two rectangles ABCD and PQRS, where side AB corresponds to side PQ, side BC corresponds to side QR, side CD corresponds to side RS, and side DA corresponds to side SP, we can write it as AB'=PQ', BC'=QR', CD'=RS', and DA'=SP'.
Corresponding sides are important because they help us determine the scale factor between two similar figures. The scale factor is the ratio of the lengths of corresponding sides. For example, if we have two similar triangles ABC and DEF, where AB/DE=BC/EF=AC/DF=k, then k is the scale factor. This means that the length of any side of one triangle is k times the length of the corresponding side of the other triangle.
Another application of corresponding sides is in solving problems involving perimeter or area. If we know the ratio of the lengths of corresponding sides, we can use it to find the ratio of the perimeters or areas. For example, if two rectangles are similar, and the ratio of their corresponding sides is 2:3, then the ratio of their perimeters is also 2:3. Similarly, the ratio of their areas is 4:9.
It's worth noting that corresponding sides are not the same as congruent sides. Congruent sides are identical in length and shape, while corresponding sides are proportional. For example, two rectangles with the same length and width are congruent, but two rectangles with different lengths and widths can still be similar and have corresponding sides.
In conclusion, corresponding sides are an essential concept in geometry that helps us identify similar figures and determine the scale factor between them. They are always proportional to each other and can be identified by matching the vertices or using the notation method. Understanding corresponding sides is crucial for solving mathematical problems and real-life applications such as architecture and engineering.
Introduction
Corresponding sides are one of the essential concepts in geometry. It is a term used to describe two sides of two different figures that are in the same relative position and have the same length. Understanding corresponding sides is crucial in many mathematical applications.
Definition of Corresponding Sides
The term corresponding means matching or in a similar position. In geometry, it refers to two sides of two different shapes that are in the same position relative to their respective shapes and have the same length. For example, if we have two triangles, one with sides of 3, 4, and 5 units, and another with sides of 6, 8, and 10 units, then the sides 3 and 6, 4 and 8, and 5 and 10 can be considered corresponding sides because they are in the same relative position and have the same length.
Importance of Corresponding Sides
Understanding corresponding sides is vital in many mathematical fields, especially in algebraic geometry and trigonometry. In algebraic geometry, corresponding sides are used to find similarities and congruence between geometric figures. In trigonometry, corresponding sides are used to calculate angles and distances between objects.
How to Identify Corresponding Sides
To identify corresponding sides, we should compare the position of each side in two different shapes. If two sides of two different shapes have the same position and length, then they are corresponding sides. We can use letters to represent the corresponding sides of two shapes. For example, if we have two triangles ABC and DEF, then the corresponding sides would be AB and DE, BC, and EF, and AC and DF.
Examples of Corresponding Sides
Let us consider an example of corresponding sides. Suppose we have two rectangles, one with a length of 6 and a width of 4 units, and another with a length of 12 and a width of 8 units. In this case, the corresponding sides would be 6 and 12 units for length and 4 and 8 units for width.
Example 1:
Triangle ABC and triangle DEF are similar triangles. Corresponding sides of these triangles are AB and DE, BC and EF, and AC and DF. If AB is 5 cm, BC is 7 cm, and AC is 8 cm, then what is the length of corresponding sides in triangle DEF?
Solution:
Since the triangles are similar, the corresponding sides are proportional. We can use the ratio of the sides of triangle ABC to find the length of corresponding sides in triangle DEF.
AB/DE = BC/EF = AC/DF
5/DE = 7/EF = 8/DF
DE = (5/8) x DF
EF = (7/8) x DF
If DF is 16 cm, then DE would be (5/8) x 16 = 10 cm, and EF would be (7/8) x 16 = 14 cm.
Example 2:
A quadrilateral ABCD has sides AB, BC, CD, and DA. A parallelogram PQRS has sides PQ, QR, RS, and SP. If AB = PQ, BC = QR, CD = RS, and DA = SP, then what is the relationship between ABCD and PQRS?
Solution:
The corresponding sides of the quadrilateral ABCD and parallelogram PQRS are equal in length. Therefore, they are congruent. We can conclude that ABCD and PQRS are congruent parallelograms.
Conclusion
Corresponding sides are an important concept in geometry that plays a significant role in many mathematical applications. Understanding corresponding sides helps us identify similarities and congruence between geometric figures and calculate angles and distances between objects.
The Basics of Corresponding Sides
Corresponding sides are sides of two or more geometric figures that are in the same relative position. They have the same orientation and shape as each other. In other words, the corresponding sides of two figures are the ones that match up with each other when the figures are placed side by side. Corresponding sides play an important role in geometry, particularly in similarity and congruence.Corresponding Sides in Plane Geometry
In plane geometry, corresponding sides are typically found in polygons. A polygon is a closed figure with three or more straight sides. When comparing two polygons, the corresponding sides are those that are opposite the same angle. For example, in the image below, the corresponding sides of the two triangles are AB and DE, BC and EF, and AC and DF.
Corresponding Sides in Solid Geometry
In solid geometry, corresponding sides are found in three-dimensional shapes such as cubes, pyramids, and prisms. When comparing two solid figures, the corresponding sides are those that have the same length and are in the same relative position. For example, in the image below, the corresponding sides of the two rectangular prisms are AB and GH, BC and FE, and AD and CG.
How Corresponding Sides are Used in Similarity
Similarity is a concept in geometry that refers to figures that have the same shape but different sizes. Corresponding sides play a key role in determining whether two figures are similar. If the corresponding sides of two figures are proportional, then the figures are similar. For example, if the sides of triangle ABC are in proportion to the sides of triangle DEF, then the two triangles are similar.The Relationship Between Corresponding Sides and Congruent Figures
Congruence is a concept in geometry that refers to figures that have the same shape and size. Corresponding sides are also important when determining whether two figures are congruent. If the corresponding sides of two figures have the same length, then the figures are congruent. For example, if triangle ABC has the same side lengths as triangle DEF, then the two triangles are congruent.Identifying Corresponding Sides in Polygons
To identify corresponding sides in polygons, you must first determine which angles are congruent. Once you have identified the congruent angles, you can then determine which sides are opposite those angles. These opposite sides are the corresponding sides of the polygons.The Role of Corresponding Sides in Trigonometry
In trigonometry, corresponding sides are used to find the values of trigonometric functions such as sine, cosine, and tangent. The ratios of the lengths of corresponding sides in right triangles are used to calculate these functions. For example, in a right triangle with angle θ, the sine of θ is equal to the length of the side opposite θ divided by the length of the hypotenuse.Understanding Similar Triangles through Corresponding Sides
Similar triangles have the same shape but different sizes. Corresponding sides play a key role in identifying similar triangles and determining the ratios of their side lengths. For example, in the image below, the corresponding sides of the two triangles are AB and DE, BC and EF, and AC and DF. If the sides are proportional, then the triangles are similar.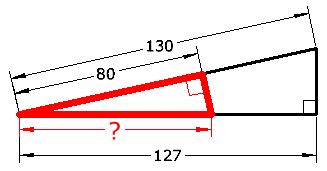
How to Calculate Corresponding Sides in Word Problems
To calculate corresponding sides in word problems, you must first identify the two figures being compared and which sides are corresponding. Once you have identified the corresponding sides, you can then use ratios to find the length of one side given the length of another. For example, if the corresponding sides of two triangles are in a ratio of 3:4, and one of the sides of the first triangle is 15 cm long, then the corresponding side of the second triangle is 20 cm long.Applications of Corresponding Sides in Real Life Situations
Corresponding sides have numerous applications in real life situations. For example, architects and engineers use corresponding sides to design structures that are similar but different sizes. Maps and blueprints also use corresponding sides to accurately represent the size and shape of buildings and geographic features. In addition, corresponding sides are used in manufacturing to create identical parts on a large scale.The Corresponding Sides Definition
Definition
The corresponding sides definition is a term used in geometry that refers to the matching sides of two similar shapes. Similar shapes are those that have the same shape but may differ in size or orientation.
Example
Let's take two similar triangles as an example. If we compare the two triangles, we can see that they have the same shape but different sizes. The corresponding sides of these two triangles are the sides that match up with each other. For example, side AB in triangle ABC corresponds to side DE in triangle DEF. Likewise, side AC corresponds to side DF and side BC corresponds to side EF.
The Corresponding Sides Definition Table:
| Keyword | Definition |
|---|---|
| Corresponding Sides | Sides in two similar shapes that match up with each other |
| Similar Shapes | Shapes that have the same shape but may differ in size or orientation |
Point of View
The corresponding sides definition is an essential concept in geometry as it helps to identify and compare the sides of similar shapes. By understanding this definition, we can easily determine which sides of two similar shapes match up with each other. This knowledge is useful in various real-life scenarios, such as scaling up or down a blueprint or creating a model of an object. In conclusion, the corresponding sides definition is a crucial element of geometry that helps us understand the relationship between similar shapes.
Closing Message: Understanding the Definition of Corresponding Sides
Thank you for taking the time to read our article about the definition of corresponding sides. We hope that this article has been informative and helpful in your understanding of this important concept in mathematics.
As we have discussed, corresponding sides are pairs of sides that are located in the same position in two similar figures. These sides have the same length and are related by a proportional relationship. Understanding this relationship is crucial in solving problems involving similar figures, which can be found in various fields, including architecture, engineering, physics, and more.
We have also covered several examples of how to identify corresponding sides in different figures, such as triangles, rectangles, and circles. By using visual aids and step-by-step explanations, we hope that you have gained a better understanding of how to apply this concept in practice.
Furthermore, we have explored some common misconceptions about corresponding sides, such as confusing them with congruent sides or assuming that they must be located in the same order in both figures. By clarifying these misunderstandings, we aim to help you avoid common errors when working with similar figures.
It is important to note that corresponding sides are just one aspect of similarity between figures. Other factors, such as corresponding angles and ratios of areas or perimeters, also play a role in determining whether two figures are similar. However, by mastering the concept of corresponding sides, you will have a solid foundation for tackling more complex problems involving similarity.
We encourage you to practice identifying corresponding sides in different figures and applying the proportional relationship between them. By doing so, you will become more confident in your ability to solve problems involving similar figures and improve your overall math skills.
If you have any questions or feedback regarding this article, please do not hesitate to leave a comment or reach out to us. We are always happy to hear from our readers and help them in their learning journey. Thank you again for reading, and we wish you all the best in your mathematical endeavors!
What is Corresponding Sides Definition?
Definition
Corresponding sides refer to the sides of two or more polygons that are in the same relative position and have the same length. In simpler terms, corresponding sides are the matching sides of two or more polygons.
Examples
For example, if you have two triangles, triangle A and triangle B, and they are both similar in shape, then their corresponding sides will be in the same proportion. For instance:
- The ratio of the length of side AB in triangle A to the length of side PQ in triangle B is equal to the ratio of the length of side BC in triangle A to the length of side QR in triangle B.
- The ratio of the length of side AC in triangle A to the length of side PR in triangle B is equal to the ratio of the length of side BC in triangle A to the length of side QR in triangle B.
These ratios will remain the same for all corresponding sides of the two triangles.
Importance
Understanding corresponding sides is important in geometry because it helps us to identify and classify geometric figures. It also allows us to solve problems that involve finding missing lengths or angles in similar polygons.
For instance, if we know the corresponding sides of two similar polygons, we can use the ratios of their lengths to find any missing side lengths. Similarly, if we know the corresponding angles of two similar polygons, we can use the ratios of their measures to find any missing angle measures.